TABLE DE MENDELEEV

Mendeleev

1.2  TABLE DE MENDELEEV

1.2.1 Introduction

Après avoir obtenu par la mécanique quantique les résultats remarquables qu'on vient d'esquisser à propos de l'atome hydrogène, il est naturel d'utiliser le même outil pour étudier les atomes plus complexes. Etablir finalement la table de Mendéléev en donnant tous les états électroniques de tous les éléments, et par conséquent leurs propriétés dans une certaine mesure, serait un travail de synthèse du plus haut intérêt.

Malheureusement, la complexité des calculs croît extrêmement vite dès que l'atome possède plus d'un électron, de sorte que le recours à des méthodes d'approximation est inéluctable. La plus simple de celles-ci, la méthode de Hartree sera décrite brièvement.

Auparavant, il faut encore rappeler deux notions importantes : le spin et le principe de Pauli. Bien que ces notions résultent chacune de théories relativement complexes, elles peuvent s'interpréter de façon simple.

1.2.2 Spin de l'électron. Définitions

Vers 1925, Uhlenbech et Goudsmit ont montré que plusieurs résultats expérimentaux non prévisibles par les théories de l'époque pouvaient être expliqués à condition d'admettre que l'électron possède un moment cinétique intrinsèque.

On appelle spin ce moment cinétique intrinsèque, noté S.

D'un point de vue classique on peut imaginer que le spin est dû à une rotation de l'électron sur lui-même. L'électron étant chargé, on admet facilement que cette rotation lui confère un moment magnétique propre, appelé moment magnétique de spin.

Bien que plausible, l'image de l'électron tournant sur lui-même doit être considérée avec prudence, car il est toujours illusoire de se représenter les phénomènes se déroulant dans l'infiniment petit à l'aide de modèles empruntés au monde à notre échelle.

Il existe un nombre quantique s associé à la projection S_z de S sur un axe z défini par exemple par un champ magnétique extérieur. Ce nombre ne peut prendre que les valeurs + 1/2 et - 1/2, il est relié à S_zpar l'expression

    (1.28)

Le spin est une notion totalement compatible avec la mécanique quantique non relativiste de Schrödinger, basée sur les équations (1.2) et (1.3). Toutefois cette mécanique ne prédit pas l'existence du spin, qui doit être introduit de manière indépendante. A partir des mêmes postulats que Schrödinger, Dirac (1929) a développé une théorie quantique relativiste qui démontre que l'électron possède un spin et que s = 1/2.

En tenant compte du spin, il faut donc quatre nombres quantiques n, l, m, s pour définir complètement l'état de l'électron dans l'atome hydrogène.

1.2.3 Occupation des niveaux d'énergie

L'étude d'atomes à plusieurs électrons révèle l'existence, comme dans le cas de l'atome hydrogène, d'un nombre théoriquement infini de niveaux d'énergies possibles pour les électrons. Le modèle de Hartree ( 1.2.7) permet encore d'associer à chacun d'eux un ensemble de quatre nombres quantiques n, l, m, s.

Dans l'état fondamental, qui est l'état correspondant à l'énergie minimum, tous les électrons devraient occuper le niveau d'énergie le plus bas. En admettant que (1.27) soit encore valable, ce niveau correspondrait à :

n =1,     l = 0,     m = 0,     s = 1/2       (1.29)

Mais l'expérience (observation des spectres) condamne radicalement cette façon de voir les choses. Dans l'état fondamental, le système des électrons possède bien l'énergie minimum possible, mais chaque électron n'a pas l'énergie minimum possible pour un électron.

En réalité, dans chaque niveau, le nombre de places disponibles pour accueillir des électrons est limité. C'est une conséquence du principe d'exclusion de Pauli.

1.2.4 Enoncé du principe d'exclusion de Pauli

On peut exprimer ce principe de manière plus ou moins générale. L'énoncé le plus simple, immédiatement utilisable dans le modèle de Hartree, est le suivant :

Dans un atome à plusieurs électrons, deux électrons ne peuvent avoir le même ensemble de nombres quantiques n , l ,m ,s.

1.2.5 Etats électroniques de l'atome d'hélium

Très simple encore, l'atome d'hélium conduit déjà à des développements mathématiques nettement plus complexes que l'atome d'hydrogène. Dans un référentiel absolu

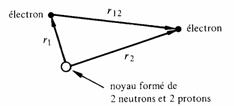
Fig. 1.8 Atome d'hélium

centré sur le noyau pour les mêmes raisons que précédemment, trois distances : r₁, r₂, r₁₂ doivent être prises en considération.

L'énergie potentielle de ce système comprend trois termes : Les deux premiers représentent l'énergie potentielle de chaque électron dans le champ du noyau, le troisième l'énergie potentielle du sous-système formé par les deux électrons. Les indices 1 et 2 servent à distinguer les électrons l'un de l'autre. En négligeant le spin, l'équation de Schrödinger prend la forme :

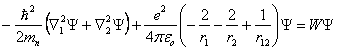                 (1.30)

Y dépend de 6 variables spatiales, qui sont les 3 coordonnées de chaque électron.

Cette équation n'est pas intégrable analytiquement, la séparation des variables est rendue impossible par la présence du terme e ²/r₁₂  représentant l'interaction électron-électron. Le recours aux méthodes numériques est donc obligatoire et parmi elles la méthode variationnelle est indiquée.

Grossièrement la procédure est la suivante, pour l'état fondamental. Une première estimation raisonnable de est établie, sur la base des solutions obtenues dans le cas de l'atome hydrogène par exemple. L'énergie du système peut alors être calculée grâce aux propriétés d'orthogonalité des fonctions d'onde. La qualité de cette première estimation doit ensuite être jugée par rapport à une deuxième estimation, q ui serait en principe plus fine. Le Théorème des variations, lequel affirme ici que la solution exacte pour Ψ minimise l'énergie, fournit le critère d'appréciation. Des algorithmes existent qui facilitent, à chaque pas, la recherche d'une fonction meilleure. Par itérations, on peut ainsi trouver une fonction d'onde aussi précise que nécessaire.

1.2.6 Etats électroniques des atomes dont Z > 2

Considérons par exemple l'atome de gallium dont l'intérêt pratique est considérable dans le domaine de l'électro-optique pour la confection de diodes luminescentes ou dans celui des installations à haute puissance où certains alliages de gallium sont utilisés comme supraconducteurs.

Bien que le gallium, qui possède 31 électrons, soit encore un élément relativement léger, la démarche adoptée pour l'hélium conduirait à une équation de Schrödinger excessivement complexe :

• La fonction dépendrait de 93 variables spatiales,
• L'énergie potentielle comprendrait 496 termes, soit 465 d'interaction électron-électron, plus 31 termes d'interaction électron-noyau.

II n'est pas possible de résoudre une telle équation dont l'existence offre davantage d'intérêt philosophique que pratique !  Dans ces conditions, une simplification du modèle atomique s'impose, et celle qu'on doit à Hartree [3] est à la base de nombreux calculs entrepris aujourd'hui dans ce domaine.

1.2.7 Modèle atomique de Hartree

L'essence de ce modèle est une méthode simplifiée pour le calcul de l'énergie d'interaction électron-électron. Au lieu de considérer individuellement et successive ment toutes les paires d'électrons possibles, Hartree fait l'hypothèse que toutes les orbitales sont sphériques. Chaque électron évolue alors dans un potentiel sphérique, somme du potentiel du noyau et de celui créé par les N-1 autres électrons. Dans cette situation, l'équation de Schrodinger pour TV électrons se laisse décomposer en adéquations pour un électron. Ces équations sont du genre de celle rencontrée pour l'atome hydrogène, à ceci près que le potentiel V(r) n'est plus en 1/r, mais d'une forme plus complexe. Un procédé d'itération permet de trouver toutes les orbitales exactes selon le modèle, à partir d'orbitales initiales choisies arbitrairement.

Solution d'équations de Schrôdinger avec un potentiel sphérique, ces orbitales sont encore identifiables par 4 nombres quantiques n, l, m, s.

L'ensemble des électrons possédant un même n constitue une couche électronique, désignée par une majuscule.

Tableau 1.9 Equivalence nombre quantique n-couche électronique

n	1	2	3	4	5	6	7
Couche	K	L	M	N	0	P	Q

Chacune de ces couches est divisée en sous-couches correspondant aux valeurs de l et désignées par des minuscules.

Tableau 1.10 Equivalence nombre quantique l-sous-couche électronique

l	0	1	2	3	4	5	6	7
Sous-couche	s	p	d	f	g	h	i	j

La configuration électronique d'un atome est donnée par la succession des sous-couches occupées. Chaque sous-couche est décrite dans la notation xa^y où a est l'identification de la sous-couche par une lettre du tableau 1.10, x la valeur de n et y le nombre d'électrons dans la sous-couche.

La configuration de l'aluminium (Z = 13) s'écrit par exemple : 1s² 2s² 2p⁶ 3s² 3p¹.

1.2.8 Energie et nombres quantiques

L'observation des spectres d'émission atomique constitue un moyen précis et puissant de comparaison des niveaux d'énergie déterminés théoriquement, avec les niveaux réels.

Malgré l'hypothèse simplificatrice relativement risquée d'un potentiel à symétrie sphérique, le modèle de Hartree fournit une prévision assez exacte des énergies des électrons appartenant à un atome. Les quatre nombres quantiques n,l,m,s servent donc souvent à répertorier ces énergies. Les variations d'énergie liées aux valeurs de m et s, beaucoup plus faibles que celles dépendant de n et l, seront négligées ici.

La figure 1.11 montre l'énergie W desél ectrons dans toutes les sous-couches formant les couches K à Q, en fonction de la charge Z du noyau, selon le modèle de Hartree. Bien que ces énergies soient représentées comme des fonctions continues, il est évident que seules les valeurs correspondant à Z entier ont une signification physique.

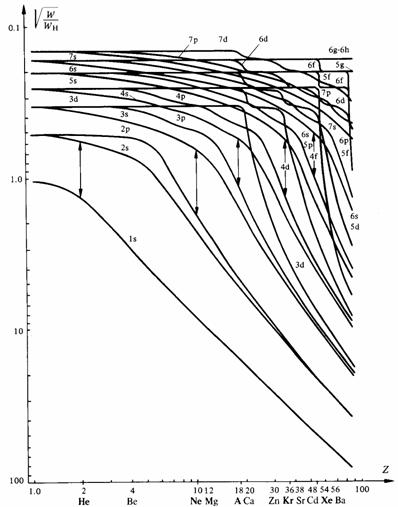
Fig 1.11 W_H représente l'énergie de l'atome H dans l'état fondamental. D'après [4].

Dans les petites valeurs de Z, par exemple Z < 18 (argon), les énergies de toutes les sous-couches d'une même couche tendent vers une même valeur lorsque Z décroît. En effet, la diminution du nombre d'électrons entraîne une diminution de l'importance relative des interactions électron-électron devant les interactions électron-noyau. Il en résulte une ressemblance croissante de l'atome considéré avec l'atome hydrogène, cas limite où seule l'interaction électron-noyau subsiste.

Dans les hautes valeurs de Z, pour n petit, c'est-à-dire dans les couches profondes, on observe une autre convergence des énergies des sous-couches d'une même couche. Celle-ci est due à l'accroissement de l'interaction électron-noyau résultant de l'augmentation de la charge de ce dernier. Les énergies des sous-couches extérieures, où l'interaction électron-électron est moins marquée par la présence du noyau, restent assez différentes les unes des autres.

Dans les valeurs intermédiaires de Z la situation est plus complexe, mais, dans une couche donnée, l'énergie augmente toujours quand l croît.

Cette règle est insuffisante pour classer toutes les sous-couches par énergie croissante. Si l'on considère la couche M par exemple, l'énergie croît quand on passe des sous-couches 3s à 3p, puis 3d, mais, ainsi qu'en témoigne la figure 1.11, l'énergie de 4s est inférieure à celle de 3d, dans une plage de Z s'étendant approximativement de 6 à 23. Les sous-couches ls, 2s, 2p, 3s, 3p comportant au total 18 électrons, la position du niveau 4s entre 3p et 3d ne peut influencer que la configuration électronique de l'état fondamental des atomes dont Z > 18. La position du niveau 4s est responsable de la structure particulière de la première série d'éléments de transition ( 1.2.14).

L'entrelacement des niveaux 3 p, 4 s et 3 d est lié au fait que l'énergie de 3 d reste constante sur un large intervalle de valeurs de Z (1 < Z < 18).

Tant que les sous-couches extérieures à 3d ne sont pas occupées, un électron se trouvant seul dans 3d est pratiquement soumis, quelle que soit l'occupation des sous-couches intérieures à 3 d, au potentiel d'un noyau virtuel portant une charge invariable e.

L'examen de la figure 1.11 montre que le cas cité n'est pas exceptionnel. Dans chaque couche dès la couche L, et de manière de plus en plus marquée quand n croît, les sous-couches correspondant aux valeurs de l les plus élevées possèdent une énergie constante sur une plage de Z de plus en plus étendue. Les entrelacements entre niveaux de couches différentes qui en résultent sont à l'origine des nombreuses irrégularités de la table de Mendéléev dont certaines forment des familles : les éléments de transition déjà cités, les terres rares, les actinides.

1.2.9 Interprétation quantique de la table de Mendéléev

Plusieurs chimistes de la seconde moitié du XIXe siècle avaient observé qu'en rangeant les éléments dans l'ordre croissant de leur poids atomique, une certaine périodicité de leurs propriétés chimiques et physiques apparaissait.

En 1869, Mendéléev dressa sa fameuse table dont l'intérêt n'a cessé de croître depuis. Si l'établissement, à l'origine intuitif, de cette table est l'un des événements les plus marquants de l'histoire de la chimie, son interprétation par la physique quantique constitue aussi une étape très importante. Au cours de celle-ci une équation d'apparence très modeste, l'équation de Schrödinger, a révélé la solution de nombreux problèmes qui avaient hanté les chimistes depuis des siècles !

L'édification théorique de la table de Mendéléev à partir des résultats du modèle de Hartree est en principe très simple. Il suffit de dénombrer les orbitales possibles par combinaison des valeurs de n, /, met s, en respectant les règles du tableau 1.3, puis de les garnir d'électrons en respectant le principe de Pauli et en choisissant, quel que soit le nombre d'électrons, la configuration correspondant à l'énergie totale minimum. Le résultat de ce travail figure au tableau 1.12. Le corps de ce tableau donne le nombre d'électrons dans les sous-couches. Ces nombres sont imprimés sur fond gris lorsque les sous-couches sont complètes.

Les propriétés chimiques d'un élément sont déterminées par le comportement des électrons qu'il possède dans la, voire les, sous-couches extérieures. Pour former des groupes d'éléments chimiquement voisins, il suffit de rassembler ceux dont la sous-couche extérieure correspond à une même valeur de l et possède le même nombre d'électrons. Dans la table de Mendéléev (tab. 1.13), ces groupes apparaissent en colonnes, à l'exception des terres rares et des actinides qui sont présentées horizontalement. Ces groupes sont traditionnellement repérés par des lettres et des chiffres romains.

Tableau 1.12

Couche		K	L		M			N				O					P				Q
Sous-couche		1s	2s	2p	3s	3p	3d	4s	4p	4d	4f	5s	5p	5d	5f	5g	6s	6p	6d	6f 6g 6h	7s
Ligne 1	1 H	1
	2 He	2
Ligne 2	3 Li	2	1
	4 Be	2	2
	5 B	2	2	1
	6 C	2	2	2
	7 N	2	2	3
	8 O	2	2	4
	9 F	2	2	5
	10 Ne	2	2	6
Ligne 3	11 Na	2	2	6	1
	12 Mg	2	2	6	2
	13 Al	2	2	6	2	1
	14 Si	2	2	6	2	2
	15 P	2	2	6	2	3
	16 S	2	2	6	2	4
	17 Cl	2	2	6	2	5
	18 Ar	2	2	6	2	6
	19 K	2	2	6	2	6		1
	20 Ca	2	2	6	2	6		2
	21 Sc	2	2	6	2	6	1	2
	22 Ti	2	2	6	2	6	2	2
	23 V	2	2	6	2	6	3	2
	24 Cr	2	2	6	2	6	5	1
	25 Mn	2	2	6	2	6	5	2
	26 Fe	2	2	6	2	6	6	2
	27 Co	2	2	6	2	6	7	2
	28 Ni	2	2	6	2	6	8	2
	29 Cu	2	2	6	2	6	10	1
	30 Zn	2	2	6	2	6	10	2
	31 Ga	2	2	6	2	6	10	2	1
	32 Ge	2	2	6	2	6	10	2	2
	33 As	2	2	6	2	6	10	2	3
	34 Se	2	2	6	2	6	10	2	4
	35 Br	2	2	6	2	6	10	2	5
	36 Kr	2	2	6	2	6	10	2	6
Ligne 5	37 Rb	2	2	6	2	6	10	2	6			1
	38 Sr	2	2	6	2	6	10	2	6			2
	39 Y	2	2	6	2	6	10	2	6	1		2
	40 Zr	2	2	6	2	6	10	2	6	2		2
	41 Nb	2	2	6	2	6	10	2	6	4		1
	42 Mo	2	2	6	2	6	10	2	6	5		1
	43 Tc	2	2	6	2	6	10	2	6	5		2
	44 Ru	2	2	6	2	6	10	2	6	7		1
	45 Rh	2	2	6	2	6	10	2	6	8		1
	46 Pd	2	2	6	2	6	10	2	6	10
	47 Ag	2	2	6	2	6	10	2	6	10		1
	48 Cd	2	2	6	2	6	10	2	6	10		2
	49 In	2	2	6	2	6	10	2	6	10		2	1
	50 Sn	2	2	6	2	6	10	2	6	10		2	2
	51 Sb	2	2	6	2	6	10	2	6	10		2	3
	52 Te	2	2	6	2	6	10	2	6	10		2	4
	53 I	2	2	6	2	6	10	2	6	10		2	5
	54 Xe	2	2	6	2	6	10	2	6	10		2	6
	55 Cs	2	2	6	2	6	10	2	6	10		2	1				1
	56 Ba	2	2	6	2	6	10	2	6	10		2	6				2
	57 La	2	2	6	2	6	10	2	6	10		2	6	1			2
	58 Ce	2	2	6	2	6	10	2	6	10	2	2	6				2
	59 Pr	2	2	6	2	6	10	2	6	10	3	2	6				2
	60 Nd	2	2	6	2	6	10	2	6	10	4	2	6				2
	61 Pm	2	2	6	2	6	10	2	6	10	5	2	6				2
	62 Sm	2	2	6	2	6	10	2	6	10	6	2	6				2
	63 Eu	2	2	6	2	6	10	2	6	10	7	2	6				2
	64 Gd	2	2	6	2	6	10	2	6	10	7	2	6	1			2
	65 Tb	2	2	6	2	6	10	2	6	10	9	2	6				2
	66 Dy	2	2	6	2	6	10	2	6	10	10	2	6				2
	67 Ho	2	2	6	2	6	10	2	6	10	11	2	6				2
	68 Er	2	2	6	2	6	10	2	6	10	12	2	6				2
	69 Tm	2	2	6	2	6	10	2	6	10	13	2	6				2
	70 Yb	2	2	6	2	6	10	2	6	10	14	2	6				2
	71 Lu	2	2	6	2	6	10	2	6	10	14	2	6	1			2
	72 Hf	2	2	6	2	6	10	2	6	10	14	2	6	2			2
	73 Ta	2	2	6	2	6	10	2	6	10	14	2	6	3			2
	74 W	2	2	6	2	6	10	2	6	10	14	2	6	4			2
	75 Re	2	2	6	2	6	10	2	6	10	14	2	6	5			2
	76 Os	2	2	6	2	6	10	2	6	10	14	2	6	6			2
	77 Ir	2	2	6	2	6	10	2	6	10	14	2	6	7			2
	78 Pt	2	2	6	2	6	10	2	6	10	14	2	6	9			1
	79 Au	2	2	6	2	6	10	2	6	10	14	2	6	10			1
	80 Hg	2	2	6	2	6	10	2	6	10	14	2	6	10			2
	81 Tl	2	2	6	2	6	10	2	6	10	14	2	6	10			2	1
	82 Pb	2	2	6	2	6	10	2	6	10	14	2	6	10			2	2
	83 Bi	2	2	6	2	6	10	2	6	10	14	2	6	10			2	3
	84 Po	2	2	6	2	6	10	2	6	10	14	2	6	10			2	4
	85 At	2	2	6	2	6	10	2	6	10	14	2	6	10			2	5
	86 Rn	2	2	6	2	6	10	2	6	10	14	2	6	10			2	6
Ligne 7	87 Fr	2	2	6	2	6	10	2	6	10	14	2	6	10			2	6			1
	88 Ra	2	2	6	2	6	10	2	6	10	14	2	6	10			2	6			2
	89 Ac	2	2	6	2	6	10	2	6	10	14	2	6	10			2	6	1		2
	90 Th	2	2	6	2	6	10	2	6	10	14	2	6	10			2	6	2		2
	91 Pa	2	2	6	2	6	10	2	6	10	14	2	6	10	2		2	6	1		2
	92 U	2	2	6	2	6	10	2	6	10	14	2	6	10	3		2	6	1		2
	93 Np	2	2	6	2	6	10	2	6	10	14	2	6	10	4		2	6	1		2
	94 Pu	2	2	6	2	6	10	2	6	10	14	2	6	10	5		2	6	1		2
	95 Am	2	2	6	2	6	10	2	6	10	14	2	6	10	6		2	6	1		2
	96 Cm	2	2	6	2	6	10	2	6	10	14	2	6	10	7		2	6	1		2
	97 Bk	2	2	6	2	6	10	2	6	10	14	2	6	10	8		2	6	1		2
	98 Cf	2	2	6	2	6	10	2	6	10	14	2	6	10	10		2	6			2
	99 E	2	2	6	2	6	10	2	6	10	14	2	6	10	11		2	6			2
	100 Fm	2	2	6	2	6	10	2	6	10	14	2	6	10	12		2	6			2
	101 Md	2	2	6	2	6	10	2	6	10	14	2	6	10	13		2	6			2
	102 No	2	2	6	2	6	10	2	6	10	14	2	6	10	14		2	6			2
	103 Lw	2	2	6	2	6	10	2	6	10	14	2	6	10	14		2	6	1		2

"Lignes de la table de Mendéléev, voir tableau 1.13

1.2.10 Gaz rares

On appelle gaz rares les éléments occupant la colonne 0, située à droite de la table de Mendéléev.

Les gaz rares, sauf l'hélium, doivent leurs propriétés au fait que leur sous-couche extérieure est complète et de type p.

La figure 1.11 montre que pour les valeurs de Z correspondant aux gaz rares, l'énergie séparant la sous-couche p de la sous-couche s suivante est très élevée. Pourtant, si l'on ajoute une ou deux unités à la valeur de Z d'un gaz rare, les électrons requis pour assurer la neutralité des nouveaux atomes vont invariablement se loger dans la sous-couche s suivante, même si des sous-couches d, f, g ou h de la même couche que p sont à disposition (tab. 1.12).

Ce fait est important, car si l'on tentait d'exciter les électrons d'un gaz rare, ils suivraient le même chemin. Les gaz rares sont donc très difficiles à exciter. Comme ils ne créent pas de champs extérieurs (tout au moins en valeur moyenne sur le temps) en raison de la symétrie de leur configuration électronique, ils sont particulièrement inaptes à former des liaisons chimiques.

Bien que ne possédant pas de sous-couche p, l'hélium est aussi un gaz rare. Il en possède les deux caractéristiques spécifiques : la prochaine sous-couche susceptible d'être occupée est de type s d'une part, elle est située à un niveau très élevé par rapport à la dernière sous-couche normalement occupée d'autre part. Simplement, celle-ci est aussi de type s alors que dans tous les autres gaz rares elle est de type p.

Les gaz rares forment une référence pertinente pour la description des autres éléments.

1.2.11 Métaux alcalins

On appelle métaux alcalins, les éléments de la colonne IA du tableau 1.13, à l'exception de l'hydrogène.

La configuration électronique d'un métal alcalin est celle d'un gaz rare à laquelle un électron a été ajouté. Cet électron occupe, ainsi qu'on vient de le voir, la sous-couche s extérieure. Il possède une énergie relativement très élevée, il est donc peu lié. C'est pourquoi les métaux alcalins sont très actifs chimiquement ( 1.3.7).

1.2.12 Métaux alcalino-terreux

Les éléments de la colonne IIA du tableau 1.13 sont appelés métaux alcalino-terreux. Leur configuration électronique est celle d'un métal alcalin à laquelle on a ajouté un électron. Leur sous-couche s extérieure est donc remplie. Ils sont plus durs et moins actifs chimiquement que les métaux alcalins avec lesquels ils forment le bloc de gauche de la table de Mendéléev.

Tableau 1.13 Table de Mendéléev

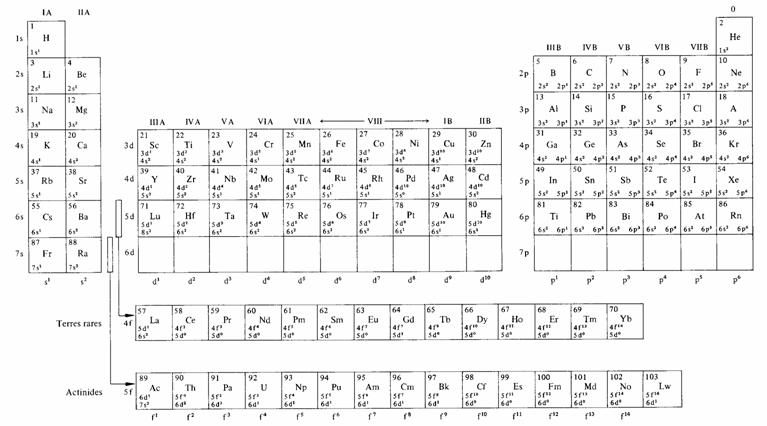
1.2.13 Halogènes

On appelle halogènes les éléments de la colonne VII B. Leur configuration électronique est celle d'un gaz rare auquel on aurait retiré un électron. Ils sont très actifs chimiquement puisqu'ils présentent un niveau vacant à une énergie relativement très basse ( 1.3.7). Le fluor est l'élément le plus actif, sous certaines conditions on serait même parvenu à le combiner à des gaz rares et à former ainsi des molécules stables.

1.2.14 Groupes III A à VI B>

En retirant des électrons de la configuration des gaz rares, jusqu'à n'en laisser plus qu'un dans la sous-couche p, on décrit les six colonnes du bloc de droite de la table de Mendéléev.

Le passage du bloc de gauche au bloc de droite est direct sur les trois premières lignes. Plusieurs propriétés des éléments, telles que l'énergie d'ionisation (c'est-à-dire l'énergie nécessaire pour retirer un électron de l'atome) ou la valence varient régulièrement sur chaque ligne, des métaux alcalins aux halogènes. Ces trois lignes épuisent les nombres atomiques compris entre 1 et 18.

Au-delà de Z = 20, des espaces supplémentaires sont nécessaires pour accueillir les éléments formés par adjonction d'électrons dans les sous-couches d ou f. Le bloc central reçoit les atomes complétant d, il comprend trois lignes correspondant aux éléments de transition de première, deuxième et troisième série. Dans chacune de ces séries, les éléments ont des énergies d'ionisation et des propriétés chimiques semblables car sauf exceptions la sous-couche extérieure, de type s, possède toujours deux électrons.

1.2.15 Terres rares et actinides

Les deux bandes horizontales situées au bas du tableau accueillent les atomes complétant f. Pour n = 4 ce sont les terres rares, pour n = 5 les actinides.

Si l'on néglige les fluctuations de l'occupation de 5 d dans les terres rares (0 ou 1 électron), et de 6 d dans les actinides (0 ou 2 électrons) l'occupation des quatre sous-couches extérieures est la même à l'intérieur de chacune de ces séries. De là résulte la similitude chimique extrême des terres rares, respectivement des actinides.