Atomes
1.1.3 Mécanique classique ou mécanique quantiqueUn système physique est correctement décrit par l'une ou l'autre des mécaniques selon l'ordre de grandeur de son action [1], ou d'autres quantités telles que son énergie ou sa temoérature. Lorsque l'action est grande vis à vis de la constante de Planck h = 6.626 10-34 J s.
1.1.4 Modèle quantique de l'atome hydrogèneL'étude élémentaire de l'atome hydrogène est basée sur les deux simplifications suivantes : • les spins ( 1.2.2) de l'électron et du proton sont omis, car leurs effets peuvent être négligés en première analyse, • le proton, environ 2 000 fois plus lourd que l'électron, est considéré comme immobile, ce qui justifie l'usage du référentiel absolu de la figure 1.2.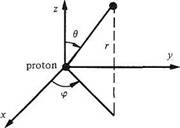
Fig. 1.2Le problème est ainsi ramené à l'analyse du comportement d'une charge ponctuelle dans un potentiel Vif) répondant ( III.3.3.1) à l'expression :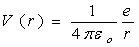 (1.1)
(1.1)
Les constantes εo et e représentent respectivement la permittivité du vide et la charge de l'électron, en valeur absolue.L'ensemble électron-proton constitue typiquement un système dont l'étude relève de la mécanique quantique. S'agissant d'un problème indépendant du temps, l'équation de Schrödinger [1] revêt la forme:
H Ψ = W Ψ (1.2)où Ψ est la fonction d'onde du système. Cette fonction dépend des coordonnées de l'espace et jouit de la propriété que Ψ2 dΩ exprime la probabilité de trouver l'électron à l'intérieur du volume dΩ. D'autre part, W représente l'énergie totale de l'électron dans l'état décrit par Ψ, et H désigne l'opérateur hamiltonien :
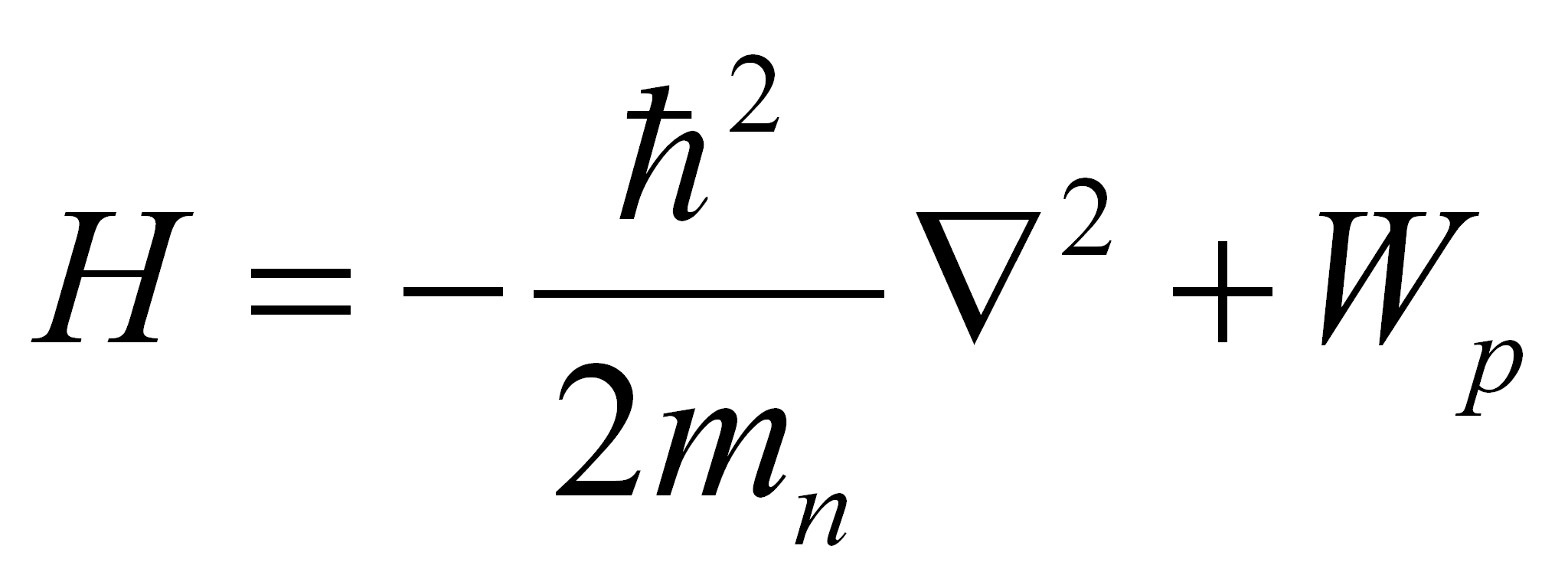 (1.3)
(1.3)
Dans cette expression, mn désigne la masse de l'électron, et Wp son énergie potentielle. Selon les notations usuelles, h"bar" = h/2π et ∇2 représente l'opérateur laplacien.
Exprimée dans le référentiel de la figure 1.2, l'équation de Schrödinger (1.2) prend la forme :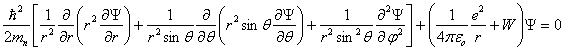 (1.4)
(1.4)
Les solutions de cette équation qui sont en accord avec les propriétés de la fonction d'onde doivent seules être retenues. En particulier :
Ψ est uniforme dans tout l'espace, doncΨ (r, θ, φ)= Ψ (r, θ, φ + 2nπ) (1.5)où n est un entier quelconque Ψ satisfait à la condition de normalisation :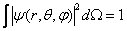 (1.6)l'intégrale portant sur tout l'espace. Cette condition implique que
(1.6)l'intégrale portant sur tout l'espace. Cette condition implique que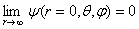 (1.7) Ψ finalement, doit être suffisamment régulière à l'origine, en particulier :
(1.7) Ψ finalement, doit être suffisamment régulière à l'origine, en particulier :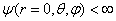 (1.8)
(1.8)
L'équation (1.4) soumise aux conditions (1.5), (1.6) et (1.8) est intégrable pour certaines valeurs de W uniquement, appelées valeurs propres. Pour chaque valeur propre, (1.4) possède en général plusieurs solutions, qui toutes peuvent être obtenues par voie purement analytique. La recherche de ces solutions est un travail assez long [2], qui se présente schématiquement de la façon suivante.La fonction d'onde est décomposée, selon la méthode de la séparation des variables, en un produit de trois fonctions R, 0, <> ne dépendant chacune que d'une variable: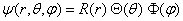 (1.9)En introduisant (1.9) dans (1.4) on obtient une équation dont un membre dépend des variables r et θuniquement, l'autre de φ uniquement. Chaque membre de cette équation doit donc être égal à une constante. En effet, si l'on fait varier seulement φ, le membre ne dépendant que de r et θ reste constant. Comme il est égal au membre ne dépendant que de φ, ce dernier est aussi une constante désignée traditionnellement par m2. Le même raisonnement s'applique pour les variations de r et θ.L'intégration du membre dépendant de φ est immédiate, elle donne :
(1.9)En introduisant (1.9) dans (1.4) on obtient une équation dont un membre dépend des variables r et θuniquement, l'autre de φ uniquement. Chaque membre de cette équation doit donc être égal à une constante. En effet, si l'on fait varier seulement φ, le membre ne dépendant que de r et θ reste constant. Comme il est égal au membre ne dépendant que de φ, ce dernier est aussi une constante désignée traditionnellement par m2. Le même raisonnement s'applique pour les variations de r et θ.L'intégration du membre dépendant de φ est immédiate, elle donne :
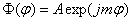 (1.10)où A est une constante d'intégration. La condition de périodicité (1.5) entraîne que m doit être entier :
(1.10)où A est une constante d'intégration. La condition de périodicité (1.5) entraîne que m doit être entier :
m = 0, 1, 2... (1.11)
En arrangeant les termes du membre fonction de r et θ, on obtient deux équations différentielles ordinaires, l'une en 0 et l'autre en r ayant chacune pour second membre une constante que la résolution de l'équation en 0 suggère d'écrire sous la forme (l + 1).Dans la recherche de Θ, on considère pour commencer m = 0. Pour que la solution soit régulière à l'origine et satisfasse (1.6), il est nécessaire que l soit un entier positif ou nul. En prenant ensuite m ≠ 0 et en conservant le résultat l est un entier positif ou nul, il apparaît que les seules solutions régulières et satisfaisant (1.6) correspondent au cas où m << l.Finalement, on trouve R par des changements de variables appropriés. Le choix des solutions acceptables fait apparaître une nouvelle constante n, ne pouvant prendre que des valeurs entières positives, inférieures ou égales à l + 1.
1.1.5 Nombres quantiques. CommentairesDans le langage des mathématiques, m, l et n caractérisent les valeurs propres des équations aux dérivées partielles pour les fonctions Φ, Θ et R, associées aux conditions de régularité à l'origine et satisfaisant (1.5) et (1.6).Les physiciens appellent m, l et n des nombres quantiques, et chacun d'eux a reçu un nom particulier (tab. 1.3).
Tableau 1.3 n = 1,2,3 Nombre quantique principal l = 0, 1,2, n-1 Nombre quantique azimutal m =0, 1, 2, ... l nombre quantique magnétique
La forme de la fonction d'onde dépendant de trois nombres quantiques, Ψ portera en indices, lorsque c'est nécessaire, les valeurs de ces trois nombres dans l'ordre n, l, m. Il en sera de même des fonctions calculées à partir de Ψ.L'image de l'atome hydrogène découlant des calculs précédents est de nature probabiliste. C'est une carte donnant, pour chaque triplet n, l, m, la probabilité d'observer l'électron en un point donné de l'espace. Plus précisément, la probabilité de trouver l'électron dans le volume dΩ entourant le point de coordonnées (r, θ, φ) vaut :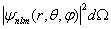 (1.12)La fonction (1.12) est représentée dans quelques cas simples aux paragraphes 1.1.7 et 1.1.10.
(1.12)La fonction (1.12) est représentée dans quelques cas simples aux paragraphes 1.1.7 et 1.1.10.
1.1.6 définition d'une orbitaleOn appelle orbitale chaque solution Ψnlm. Une orbitale décrit complètement l'électron dans l'état correspondant aux valeurs spécifiées des trois nombres quantiques. C'est-à-dire qu'elle contient toutes les informations qu'il est possible de connaître sur l'électron, telles que sa position, son énergie cinétique, son énergie potentielle.
1.1.7 Orbitale de l'atome hydrogène dans l'état fondamentalPar définition, l'état fondamental est l'état d'énergie minimum. Il correspond au cas n = 1, l = 0, m = 0. La fonction d'onde se réduit à
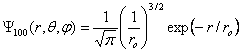 (1.13)où
(1.13)où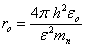 (1.14)La probabilité d'observer l'électron à une distance comprise entre r et r + dr du noyau vaut :
(1.14)La probabilité d'observer l'électron à une distance comprise entre r et r + dr du noyau vaut :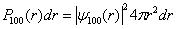 (1.15)La distance la plus probable de l'électron au noyau s'obtient en cherchant la valeur de r rendant maximum P(r) :
(1.15)La distance la plus probable de l'électron au noyau s'obtient en cherchant la valeur de r rendant maximum P(r) :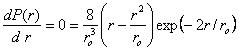 (1.16)d'oùr = r0 (1.17)On appelle r0 le rayon de la première orbite de Bohr. D'après (1.14) r0 = 0,0529 nm.Cette notion d'orbite ne doit pas être interprétée d'une façon déterministe et rigide. L'orbite est simplement le lieu géométrique des points où la probabilité de trouver l'électron est maximum (fig. 1.4).
(1.16)d'oùr = r0 (1.17)On appelle r0 le rayon de la première orbite de Bohr. D'après (1.14) r0 = 0,0529 nm.Cette notion d'orbite ne doit pas être interprétée d'une façon déterministe et rigide. L'orbite est simplement le lieu géométrique des points où la probabilité de trouver l'électron est maximum (fig. 1.4).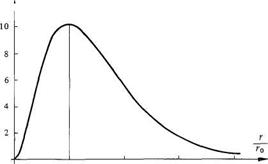 Fig. 1.4 Densité de probabilité de trouver l'électron à une distance r du noyau. (1.15)
Fig. 1.4 Densité de probabilité de trouver l'électron à une distance r du noyau. (1.15)
1.1.8 Rayon de l'atome hydrogène dans l'état fondamentalOn peut admettre que le rayon de l'atome est égal à la distance r du noyau à l'électron. Un spectateur constaterait qu'à chaque observation, le rayon de l'atome prend une valeur différente, mais qu'il reste le plus souvent proche de r0. Le rayon de l'atome est une variable aléatoire dont la valeur la plus probable est r0.Pour illustrer les fluctuations de r, il est intéressant de calculer la probabilité d'observer un atome de rayon 0,1 r0, puis 10 r0. En rapportant ces probabilités à celles d'observer un atome de rayon r0 on a, d'après (1.15) :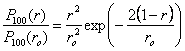 (1.18)D'où
(1.18)D'où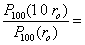 1.52 10-6 et
1.52 10-6 et 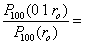 6.05 10-6 (1.19)En chiffres rond, on a donc une chance sur 17 d'observer un atome de rayon r = 0,1 ro, et une chance sur 658000 d'observer un atome de rayon r = 10 ro
6.05 10-6 (1.19)En chiffres rond, on a donc une chance sur 17 d'observer un atome de rayon r = 0,1 ro, et une chance sur 658000 d'observer un atome de rayon r = 10 ro
1.1.9 Energie W de l'atome hydrogène dans l'état fondamentalCette énergie apparaît ( 1.1.4) comme une valeur propre de (1.4), lors de l'intégration de cette équation menant à la fonction d'onde Ψ100. Le détail des calculs n'ayant pas été présenté, il est intéressant de retrouver maintenant cette énergie en introduisant la solution Ψ100 dans (1.4). Dans le cas présent où la fonction d'onde ne dépend pas de θ ni de φ, l'équation (1.4) se réduit à :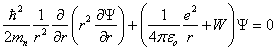 (1.20)En posant Ψ = Ψ100 dans cette équation et en écrivant pour simplifier
(1.20)En posant Ψ = Ψ100 dans cette équation et en écrivant pour simplifier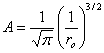 (1.21)
(1.21)
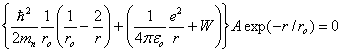 (1.22)Cette équation doit être satisfaite pour toute valeur positive de r différente de zéro, il s'ensuit que les coefficients de 1/r exp (~r/r0) d'une part, et de exp (-r/ro d'autre part doivent être nuls. Cela conduit aux relations suivantes, respectivement :
(1.22)Cette équation doit être satisfaite pour toute valeur positive de r différente de zéro, il s'ensuit que les coefficients de 1/r exp (~r/r0) d'une part, et de exp (-r/ro d'autre part doivent être nuls. Cela conduit aux relations suivantes, respectivement :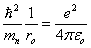 > (1.23)et
> (1.23)et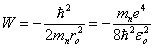 (1.24)
(1.24)
La première n'apporte rien de nouveau puisqu'elle fournit une nouvelle fois la valeur de ro donnée par (1.14). Par la seconde on calcule :W = -2,18 10-18J = -13,6eV (1.25)Des expériences de spectroscopie avaient montré bien avant 1928 (équation de Schrödinger) que le niveau énergétique le plus bas de l'atome hydrogène était précisément de - 13,6 eV. Ce fut un succès considérable pour la mécanique quantique naissante d'avoir retrouvé cette valeur par une voie purement théorique.
1.1.10 Orbitales de l'atome hydrogène dans un état excité. Cas particuliersOn considère ici les cas ou n est quelconque, alors que l= 0 et m = 0. La fonction d'onde garde alors une symétrie sphérique et prend la forme :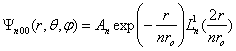 (1.26)où
(1.26)où  est un polynôme associé de Laguerre, du premier ordre et de degré n - 1 (sect. 7.1). La densité de probabilité de trouver l'électron à une distance r du noyau Pnoo (r) est représentée à la figure 1.5. On remarque que cette fonction présente un nombre de maxima égal à n, et que le rayon le plus probable augmente avec n.
est un polynôme associé de Laguerre, du premier ordre et de degré n - 1 (sect. 7.1). La densité de probabilité de trouver l'électron à une distance r du noyau Pnoo (r) est représentée à la figure 1.5. On remarque que cette fonction présente un nombre de maxima égal à n, et que le rayon le plus probable augmente avec n.
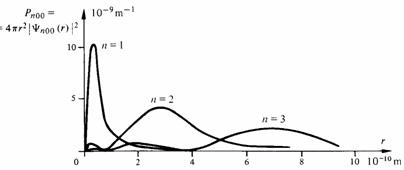 Fig. 1.5L'énergie Wn de l'atome est donnée par :
Fig. 1.5L'énergie Wn de l'atome est donnée par :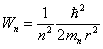 (1.27)
(1.27)
On vérifie que cette expression se confond avec (1.24) si n = 1, D'autre part, on montre que (1.27) reste valable dans le cas général où n, l et m sont quelconques.
L'interprétation de ce qui précède est simple. Quand n croît, l'énergie de l'électron, négative, s'approche de zéro. Or, l'expression (1.1) utilisée pour décrire le potentiel V(r) implique qu'un électron libre au repos possède une énergie nulle. Donc, plus n est grand, moins l'électron est lié au noyau et plus grand est le rayon le plus probable de l'atome.
1.1.11 Orbitales de l'atome hydrogène, cas généralDès que l > = 1 les orbitales et la densité de probabilité Pnlm = Ψnlm2 présentent une dépendance angulaire. Toutefois la forme de Φ, donnée par l'équation (1.10), montre que Pnlm reste indépendant de φet garde donc une symétrie de rotation autour de l'axe z. C'est pourquoi il est d'usage de représenter Pnlm> dans un diagramme polaire (fig. 1.6) tracé dans un plan contenant l'axe z.
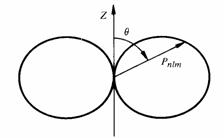 Fig. 1.6
Fig. 1.6
L'allure de Pnlm se complique rapidement dès que l croît, comme en témoigne la figure 1.7 où l'on a représenté schématiquement toutes les formes de cette fonction pour l = 3.
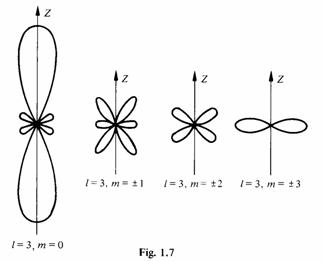
1.1.12 CommentaireDans les atomes plus lourds que l'hydrogène la densité de probabilité présente des lobes semblables à ceux de la figure 1.7, quoique de forme encore plus complexe. L'existence de ces lobes joue un rôle très important dans de nombreux domaines, tel celui de la valence (sect. 1.3) ou celui de la liaison de super-échange ( 3.5.3), pour ne citer que ces exemples.
1.1.3 Mécanique classique ou mécanique quantique
Un système physique est correctement décrit par l'une ou l'autre des mécaniques selon l'ordre de grandeur de son action [1], ou d'autres quantités telles que son énergie ou sa temoérature. Lorsque l'action est grande vis à vis de la constante de Planck h = 6.626 10-34 J s.
1.1.4 Modèle quantique de l'atome hydrogène
L'étude élémentaire de l'atome hydrogène est basée sur les deux simplifications suivantes :
• les spins ( 1.2.2) de l'électron et du proton sont omis, car leurs effets peuvent être négligés en première analyse,
• le proton, environ 2 000 fois plus lourd que l'électron, est considéré comme immobile, ce qui justifie l'usage du référentiel absolu de la figure 1.2.
 |
Fig. 1.2
Le problème est ainsi ramené à l'analyse du comportement d'une charge ponctuelle dans un potentiel Vif) répondant ( III.3.3.1) à l'expression :
Les constantes εo et e représentent respectivement la permittivité du vide et la charge de l'électron, en valeur absolue.
L'ensemble électron-proton constitue typiquement un système dont l'étude relève de la mécanique quantique. S'agissant d'un problème indépendant du temps, l'équation de Schrödinger [1] revêt la forme:
H Ψ = W Ψ (1.2)
où Ψ est la fonction d'onde du système. Cette fonction dépend des coordonnées de l'espace et jouit de la propriété que Ψ2 dΩ exprime la probabilité de trouver l'électron à l'intérieur du volume dΩ. D'autre part, W représente l'énergie totale de l'électron dans l'état décrit par Ψ, et H désigne l'opérateur hamiltonien :
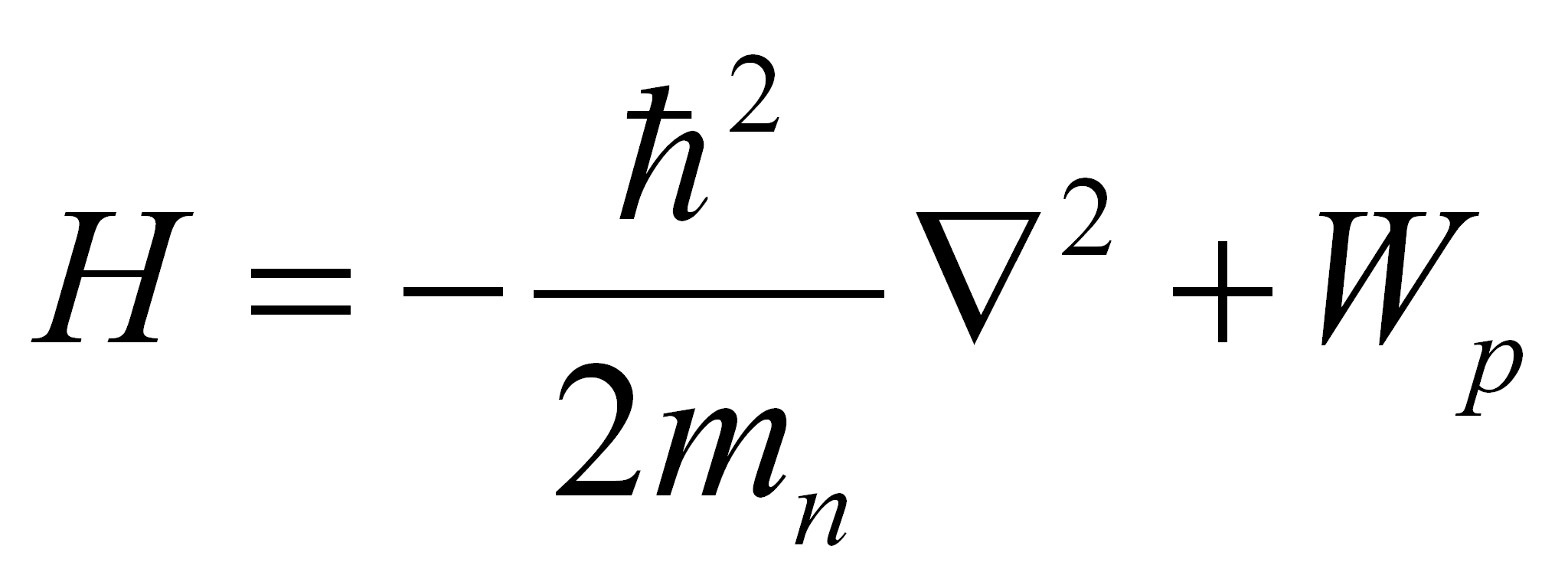 (1.3)
(1.3)Dans cette expression, mn désigne la masse de l'électron, et Wp son énergie potentielle. Selon les notations usuelles, h"bar" = h/2π et ∇2 représente l'opérateur laplacien.
Exprimée dans le référentiel de la figure 1.2, l'équation de Schrödinger (1.2) prend la forme :
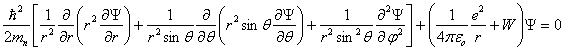 (1.4)
(1.4)Les solutions de cette équation qui sont en accord avec les propriétés de la fonction d'onde doivent seules être retenues. En particulier :
Ψ est uniforme dans tout l'espace, donc
Ψ (r, θ, φ)= Ψ (r, θ, φ + 2nπ) (1.5)
où n est un entier quelconque
Ψ satisfait à la condition de normalisation :
l'intégrale portant sur tout l'espace. Cette condition implique que
Ψ finalement, doit être suffisamment régulière à l'origine, en particulier :
L'équation (1.4) soumise aux conditions (1.5), (1.6) et (1.8) est intégrable pour certaines valeurs de W uniquement, appelées valeurs propres. Pour chaque valeur propre, (1.4) possède en général plusieurs solutions, qui toutes peuvent être obtenues par voie purement analytique. La recherche de ces solutions est un travail assez long [2], qui se présente schématiquement de la façon suivante.
La fonction d'onde est décomposée, selon la méthode de la séparation des variables, en un produit de trois fonctions R, 0, <> ne dépendant chacune que d'une variable:
En introduisant (1.9) dans (1.4) on obtient une équation dont un membre dépend des variables r et θuniquement, l'autre de φ uniquement. Chaque membre de cette équation doit donc être égal à une constante. En effet, si l'on fait varier seulement φ, le membre ne dépendant que de r et θ reste constant. Comme il est égal au membre ne dépendant que de φ, ce dernier est aussi une constante désignée traditionnellement par m2. Le même raisonnement s'applique pour les variations de r et θ.
L'intégration du membre dépendant de φ est immédiate, elle donne :
où A est une constante d'intégration. La condition de périodicité (1.5) entraîne que m doit être entier :
m = 0, 1, 2... (1.11)
En arrangeant les termes du membre fonction de r et θ, on obtient deux équations différentielles ordinaires, l'une en 0 et l'autre en r ayant chacune pour second membre une constante que la résolution de l'équation en 0 suggère d'écrire sous la forme (l + 1).
Dans la recherche de Θ, on considère pour commencer m = 0. Pour que la solution soit régulière à l'origine et satisfasse (1.6), il est nécessaire que l soit un entier positif ou nul. En prenant ensuite m ≠ 0 et en conservant le résultat l est un entier positif ou nul, il apparaît que les seules solutions régulières et satisfaisant (1.6) correspondent au cas où m << l.
Finalement, on trouve R par des changements de variables appropriés. Le choix des solutions acceptables fait apparaître une nouvelle constante n, ne pouvant prendre que des valeurs entières positives, inférieures ou égales à l + 1.
1.1.5 Nombres quantiques. Commentaires
Dans le langage des mathématiques, m, l et n caractérisent les valeurs propres des équations aux dérivées partielles pour les fonctions Φ, Θ et R, associées aux conditions de régularité à l'origine et satisfaisant (1.5) et (1.6).
Les physiciens appellent m, l et n des nombres quantiques, et chacun d'eux a reçu un nom particulier (tab. 1.3).
| Tableau 1.3 | |
| n = 1,2,3 | Nombre quantique principal |
| l = 0, 1,2, n-1 | Nombre quantique azimutal |
m =0, 1, 2, ... l | nombre quantique magnétique |
La forme de la fonction d'onde dépendant de trois nombres quantiques, Ψ portera en indices, lorsque c'est nécessaire, les valeurs de ces trois nombres dans l'ordre n, l, m. Il en sera de même des fonctions calculées à partir de Ψ.
L'image de l'atome hydrogène découlant des calculs précédents est de nature probabiliste. C'est une carte donnant, pour chaque triplet n, l, m, la probabilité d'observer l'électron en un point donné de l'espace. Plus précisément, la probabilité de trouver l'électron dans le volume dΩ entourant le point de coordonnées (r, θ, φ) vaut :
La fonction (1.12) est représentée dans quelques cas simples aux paragraphes 1.1.7 et 1.1.10.
1.1.6 définition d'une orbitale
On appelle orbitale chaque solution Ψnlm. Une orbitale décrit complètement l'électron dans l'état correspondant aux valeurs spécifiées des trois nombres quantiques. C'est-à-dire qu'elle contient toutes les informations qu'il est possible de connaître sur l'électron, telles que sa position, son énergie cinétique, son énergie potentielle.
1.1.7 Orbitale de l'atome hydrogène dans l'état fondamental
Par définition, l'état fondamental est l'état d'énergie minimum. Il correspond au cas n = 1, l = 0, m = 0. La fonction d'onde se réduit à
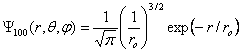 (1.13)
(1.13)où
La probabilité d'observer l'électron à une distance comprise entre r et r + dr du noyau vaut :
La distance la plus probable de l'électron au noyau s'obtient en cherchant la valeur de r rendant maximum P(r) :
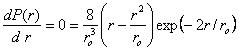 (1.16)
(1.16)d'où
r = r0 (1.17)
On appelle r0 le rayon de la première orbite de Bohr. D'après (1.14) r0 = 0,0529 nm.
Cette notion d'orbite ne doit pas être interprétée d'une façon déterministe et rigide. L'orbite est simplement le lieu géométrique des points où la probabilité de trouver l'électron est maximum (fig. 1.4).

Fig. 1.4 Densité de probabilité de trouver l'électron à une distance r du noyau. (1.15)
1.1.8 Rayon de l'atome hydrogène dans l'état fondamental
On peut admettre que le rayon de l'atome est égal à la distance r du noyau à l'électron. Un spectateur constaterait qu'à chaque observation, le rayon de l'atome prend une valeur différente, mais qu'il reste le plus souvent proche de r0. Le rayon de l'atome est une variable aléatoire dont la valeur la plus probable est r0.
Pour illustrer les fluctuations de r, il est intéressant de calculer la probabilité d'observer un atome de rayon 0,1 r0, puis 10 r0. En rapportant ces probabilités à celles d'observer un atome de rayon r0 on a, d'après (1.15) :
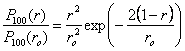 (1.18)
(1.18)D'où
En chiffres rond, on a donc une chance sur 17 d'observer un atome de rayon r = 0,1 ro, et une chance sur 658000 d'observer un atome de rayon r = 10 ro
1.1.9 Energie W de l'atome hydrogène dans l'état fondamental
Cette énergie apparaît ( 1.1.4) comme une valeur propre de (1.4), lors de l'intégration de cette équation menant à la fonction d'onde Ψ100. Le détail des calculs n'ayant pas été présenté, il est intéressant de retrouver maintenant cette énergie en introduisant la solution Ψ100 dans (1.4). Dans le cas présent où la fonction d'onde ne dépend pas de θ ni de φ, l'équation (1.4) se réduit à :
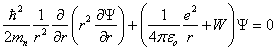 (1.20)
(1.20)En posant Ψ = Ψ100 dans cette équation et en écrivant pour simplifier
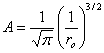 (1.21)
(1.21)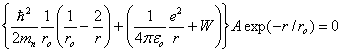 (1.22)
(1.22)Cette équation doit être satisfaite pour toute valeur positive de r différente de zéro, il s'ensuit que les coefficients de 1/r exp (~r/r0) d'une part, et de exp (-r/ro d'autre part doivent être nuls. Cela conduit aux relations suivantes, respectivement :
et
La première n'apporte rien de nouveau puisqu'elle fournit une nouvelle fois la valeur de ro donnée par (1.14). Par la seconde on calcule :
W = -2,18 10-18J = -13,6eV (1.25)
Des expériences de spectroscopie avaient montré bien avant 1928 (équation de Schrödinger) que le niveau énergétique le plus bas de l'atome hydrogène était précisément de - 13,6 eV. Ce fut un succès considérable pour la mécanique quantique naissante d'avoir retrouvé cette valeur par une voie purement théorique.
1.1.10 Orbitales de l'atome hydrogène dans un état excité. Cas particuliers
On considère ici les cas ou n est quelconque, alors que l= 0 et m = 0. La fonction d'onde garde alors une symétrie sphérique et prend la forme :
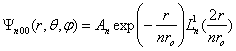 (1.26)
(1.26)où 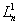 est un polynôme associé de Laguerre, du premier ordre et de degré n - 1 (sect. 7.1). La densité de probabilité de trouver l'électron à une distance r du noyau Pnoo (r) est représentée à la figure 1.5. On remarque que cette fonction présente un nombre de maxima égal à n, et que le rayon le plus probable augmente avec n.
est un polynôme associé de Laguerre, du premier ordre et de degré n - 1 (sect. 7.1). La densité de probabilité de trouver l'électron à une distance r du noyau Pnoo (r) est représentée à la figure 1.5. On remarque que cette fonction présente un nombre de maxima égal à n, et que le rayon le plus probable augmente avec n.

Fig. 1.5
L'énergie Wn de l'atome est donnée par :
On vérifie que cette expression se confond avec (1.24) si n = 1, D'autre part, on montre que (1.27) reste valable dans le cas général où n, l et m sont quelconques.
L'interprétation de ce qui précède est simple. Quand n croît, l'énergie de l'électron, négative, s'approche de zéro. Or, l'expression (1.1) utilisée pour décrire le potentiel V(r) implique qu'un électron libre au repos possède une énergie nulle. Donc, plus n est grand, moins l'électron est lié au noyau et plus grand est le rayon le plus probable de l'atome.
1.1.11 Orbitales de l'atome hydrogène, cas général
Dès que l > = 1 les orbitales et la densité de probabilité Pnlm = Ψnlm2 présentent une dépendance angulaire. Toutefois la forme de Φ, donnée par l'équation (1.10), montre que Pnlm reste indépendant de φet garde donc une symétrie de rotation autour de l'axe z. C'est pourquoi il est d'usage de représenter Pnlm> dans un diagramme polaire (fig. 1.6) tracé dans un plan contenant l'axe z.

Fig. 1.6
L'allure de Pnlm se complique rapidement dès que l croît, comme en témoigne la figure 1.7 où l'on a représenté schématiquement toutes les formes de cette fonction pour l = 3.

1.1.12 Commentaire
Dans les atomes plus lourds que l'hydrogène la densité de probabilité présente des lobes semblables à ceux de la figure 1.7, quoique de forme encore plus complexe. L'existence de ces lobes joue un rôle très important dans de nombreux domaines, tel celui de la valence (sect. 1.3) ou celui de la liaison de super-échange ( 3.5.3), pour ne citer que ces exemples.













Aucun commentaire:
Enregistrer un commentaire
bienvenu